Optimization of Gas Lift Allocation Using Different Models-Juniper Publishers
Juniper Publishers
Abstract
Gas lift for oil-gas extraction is a common
practice; however, obtaining maximum productivity of a series of set is
not a simple tax because high amount of gas lift makes the optimization
of few wells at the same time a very hard task. Therefore, data
processing approaches based on calculations and computerized modeling
has been receiving attention. By modeling well, it could be possible to
obtain higher production rate versus less gas consumption. The present
paper is a new approach that uses neural functions and genetic algorithm
and studies the different aspects of problem solving for gas allocation
optimization in five wells. The results showed that artificial neural
networks have very good function in modeling gas lift process and
creating gas lift performance curve versus classic methods. The
differences between the results obtained by artificial neural network in
comparison with results that are obtained in classic methods prove this
claim.
Keywords: Genetic algorithm; Artificial neural network; Gas lift; Allocation optimizationIntroduction
The normal yield of an oil well does not meet the
demands of oil industry due to increasing rate of collection. For that
reason, using some methods for increasing collection is inevitable. Pump
and gas lift is one of the artificial lift approaches; however, it
could not be used in all wells with maximum power due to energy
consumption problem. In another word, gas lift in a series of well by
optimization of the approach is an economic-functional issue [1].
Studying gas lift is usually performed by using gas
lift performance curve. For the first time, Roy & Cataporan [2] used
an analytical method to create gas lift performance curve in a well.
This curve is obtained by drawing the data of oil collection values vs.
gas lift amount [3].
There are various methods for fitting the gas lift
performance curve; including line fitting by using regression and
obtaining equation coefficient. The regression method by calculating
equation coefficient is a relatively simple method for modeling gas lift
performance in oil wells; however, it lacks flexibility and does not
pay attention to the nature of data and their logic; therefore, it is
opt to be erroneous in using for different wells. In another word, the
same model could not be used in all wells. Modeling based on artificial
neural network is an approach that could be discussed due to considering
the logic of data and withdrawal from placing the data in a cliché
frame. The artificial neural network, which is mostly called as neural
network in brief, is
a mathematical model that acts by being inspired form human neural
system [4].
A neural network consist of one or few groups of
artificial connected neural cells that process data by using connective
and interactive methods. In most cases, neural networks lack
compatibility system; that is, changes in their structure take place in
learning phase and they improve themselves for modeling. Artificial
neural networks have already been used in modeling complicated relations
between inputs and outputs/entry-exits and finding existing patterns in
data. For gas lift optimization too, these functions have been used for
lift optimization particularly when it was difficult to obtain
mathematical functions [5].
The genetic algorithm (GA) is an explorative search method
that copies the natural evolution process. The algorithm model
relies on repetitions and using that repetition and accident
in genetic algorithm to optimize production and search for
maximum power. In another word, GA belongs to a larger
class known as evolutionary algorithms that is a solution for
optimization problems by using the evolutionary techniques
such as inheritance, mutation, selection and etc. [6].
GA has application in bioinformatics, calculation
disciplines, engineering, economic, mathematics, physics and
other areas. There is a history of using GA in optimizing gas
allocation of a single well or a series of few wells. Martinez
used this algorithm for the first time for optimization of gas
lift collection [7].
A combination of neural network as a model and GA as
an optimizer could be used in solving optimization issues.
In 1999, Stoisits et al used modeling of a series of well with
neural network and optimizing it with GA. Their perspective
in using this optimization system was more in the direction
of operational parameters such as the pressure of well and
lacked the intensive economical aspect [8]. In present paper,
five neural models are linked to a GA with suitable inputs for
optimizing the five wells at the same time under different
operational conditions and the economy of the process has
been summed up as well.
Development of Gas Lift Performance Curve by Modeling with Neural Network
Many models have been suggested for modeling the
amount of oil collection against gas lift. For example, second
degree model is one of those models that due to unsymmetrical
form of gas lift performance curve, it does not create suitable
fitting [9]. For this reason, other models have been suggested
by the researchers of this field. Alarcon et al. [10] in 2002
and Khishvand [11] tried to determine a suitable model. The
Alarcon’s model (equation 1) and Khishvand (equation 2) are
as follows:
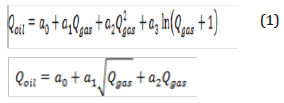
For modeling with the neural network, a multi-layer feedforward
network with 4 hidden layers with 10 tansig neurons in
each layer was used. Then, the results of fitting the two models
mentioned above (equations 1 and 2) were used to compare
the function of the neural network model vs. mentioned classic
methods. The results are listed in (Table 1).
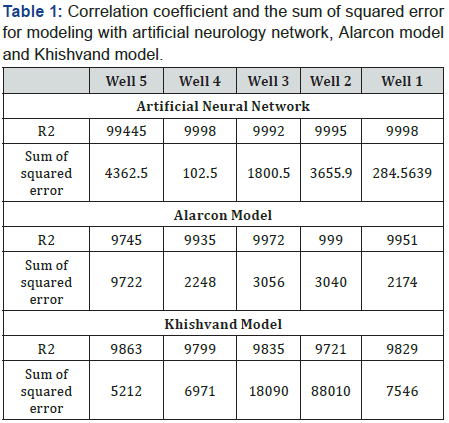
The results of Table 1 show that the artificial neural network,
Alarcon and Khishvand model has desire fitness. In addition,
as Table 1 shows, the highest correlation coefficient and
lowest sum of squared errors were obtained by artificial
neural networks. Khishvand’s model showed weaker results
in comparison with Alarcon model on the wells subject of this
paper.
It should be mentioned that the above-mentioned result
were obtained by using the most usual neural networks
without manipulating geometric parameters of the network.
Therefore, most probably, by designing network and using
more data, those results could be improved considerably. In
continuation, the results of drawing gas lift performance curve
by using artificial neural networks for five wells are shown
(Figure 1).
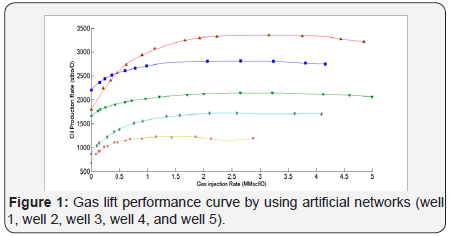
In Figure 1, the marked dots show the empirical values and
the corresponding line of each set of knot shows the neural
network model of each well. As it is shown and could be seen
in (Table 1) too, suitable agreement of the empirical values
and artificial neural network could be seen. On the other hand,
by using the model of each one of the wells, quantities such as minimum collection of each well, maximum collection of each
well and potential for additional collection of each well could
be obtained. This information was obtained for all five wells
and is listed in (Table 2).
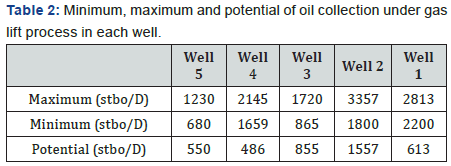
The amount of potential of increasing collection in the
process of gas lift has been obtained by differentiating the
maximum collection with gas lift and collection in no gas lift
conditions. This parameter is independent from gain without
gas lift; that is, primary conditions of wells. Due to studying
optimized answers, it is interesting to calculate this parameter
in order to find out how much the gas allocation between
wells in an optimized state would be in relationship with the
potential of the wells involved in optimization.
Unrestricted Optimization of Gas Allocation In Wells and Its Effects on Total Collection
There are different approaches in optimization of a series
of well [11]. The approaches could endure different restrictions
on the optimization issue. I any way, restrictions such as the
range of gas imposing to each well are necessary and inevitable
while restrictions such as entry gas originates from economic
necessities and studying them is a farther priority than the
conditions of gas lift for each well. In this study, we used a
trained neural function and linking it to genetic algorithm
tool box to optimize the amount of oil production of a series of
well and studying the factors. We benefitted from the method
of developing the total utilization function and the target
function in our issue in most simple situation was maximum
total production. This target function could be solved per case
without boundaries. For example, the genetic algorithm could
be used to obtain maximum total production when less gas
lift complex is accessible. In continuation, development and
solving little suitable target function is discussed by using
common concept in the literature of this discipline and some
new suggestions are proposed as well.
Development of the Target Function Of Total Production without Economic Boundaries and Restriction
In this situation, optimization of the sum of wells production
will be performed, conditioned by using the amount of gas
lift in the scope of model information. The proposed target
function and its requisite are described in equations 3 and 4.
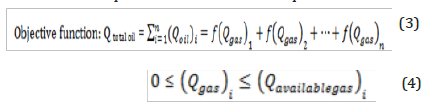
Development of the target function of total production by economic restriction and studying the effects of economic restriction in productivity
This situation is like previous one with the difference
that the sum of entering gas should be less than or equal to a
constant amount. In practice, the sum of lift gas should be less
than the amount of gas in access. In addition, high costs of the
gas make this value to be as low as possible.
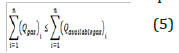
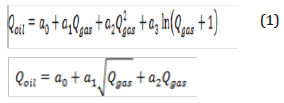
The amount of accessible gas might differ as per operational
conditions and therefore, it is interesting to study the effects of
gas restriction on the maximum collection conditions. To study
this, GA was used. Figure 2 shows the results (55 points) of the
calculations. As diagram in (Figure 2) shows, change in total
production vs. restriction in total gas lift had an initially strong
function and by the increase in amount of gas, the amount of
changes and functionality vs. amount of lift restriction reduces
accordingly.
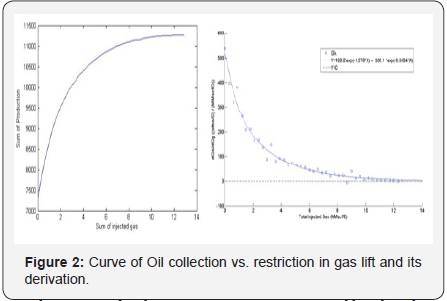
This means that by increasing as to optimized level without
restriction (last point in curve), the amount of production
increase against consumed gas will be so trivial that would not
have economic justification. Hatton et al; too, in studying a field
with one hundred wells obtained similar results [12]. In many
papers, the limit of 3 million cubic foot standard (MMscf/D)
has been defined for total gas arrival in access and observing
those conditions in our study could led to 27% increase in
oil production. Due to the importance of using least gas and
obtaining highest output, it is important to determine the
suitable degree of lift restriction. In following parts, two target
functions have been proposed for economic optimization and
their results are compared.
Suggestion of Production Target Functions for Achieving Economic Optimizations
The amount of oil production increase per gas consumption
unit could be considered as an important index in lifting operations and the largeness of number leads to economic
productivity of the oil field. For this reason, this index could
be considered as target function to be maximized by using
genetic algorithm. For this purpose, two target functions are
suggested: The function of sum of net productions of wells and
the function of net production of wells and their only difference
is in the method of modeling for gas lift production. The
function of sum of net production of wells is defined as follows:
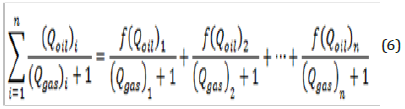
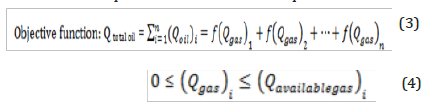
In addition, total net production function is standardized
as follows:
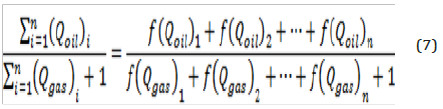
Economic- performance desirability of the conditions
obtained from each target function could be defined with
respect to the increase in production divided into sum of
lift gas in optimized state. The scale is million cubic foot
standard in one power (1/stbd/D). In this case, the boundless
optimization desirability of wells will be 2.75 (percent
collection improvement/ amount of lift gas), the desirability
obtained from optimization function of sum of net production
of wells (equation 6) is 17.15 and desirability of optimization
of total net production (equation 7) will be 21.59. On the other
hand, in many papers, the restricted optimization or maximum
accessible gas was concerned while in our study, by including
lift restriction of total 3 million cubic foot standard gas per day,
the perspective will end to desirability value of 9 which is less
than the desirability of suggested target functions.
Therefore, it could be claimed that it is not economical to
use all the gas accessible for gas lift project and optimizing the
amount of gas lift is a delicate issue; therefore, modeling with
neural network and optimizing with GA could be a solution.
Another interesting point is the approach of gas allocation
by genetic algorithm. The arrangement of potentials magnitude
of wells subject of study is as follows: well 2, well 3, well 1, well
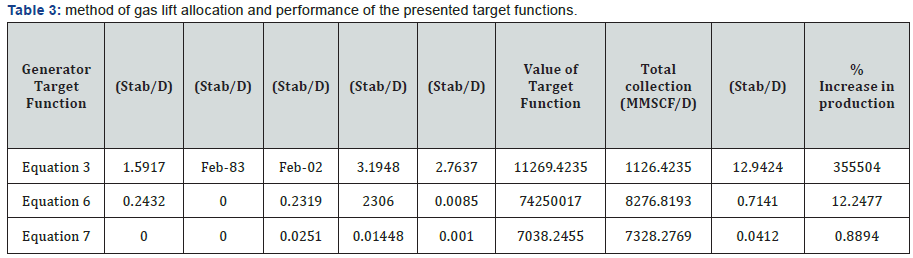
5 and well 4. In optimizing with target function in equations 6
and 7, as Table 3 shows, wells 4, 5 and 1 were not gas lifted and
since those functions (equations 6 and 7) show the desirable economic point too, it seems that GA has withdrawn from
optimizing the mentioned wells for maximizing economic
profit.
It is highly interesting that the mentioned wells were
among the poorest wells in the issue and potential in terms
of parameter and this shows the importance of potential
parameters in gas lift optimization process; because, if only
highly potential wells are selected as gas under lift process,
most probably, this would lead the load of optimization
calculation load and increase in lift output.
Effects of the Number Of Wells Involved In Gas Allocation Optimization
Resource management in a gas lift project could be
performed in various forms. The number of wells in optimization
process is one of the issues that are important in this regards.
As an example, in a gas lift network with five wells, the subject
could be handled in one of the following approaches:
- Optimization of all five wells by using restriction of sum of input gas
- Optimization of a number of wells without restriction and not optimizing other wells
- Optimization of a number of wells with the restriction in total entry gas and not optimizing other well
The first scenario has been receiving more anticipation;
however, scenarios 2 and 3 did not seem much favorable and
of course, no suitable comparative study has been performed
regarding those approaches. The logic of the first scenarios
is its attention to all wells proportion to their potential and
economic abilities. In addition, scenario 2 and 3 are elite
adoption scenarios and supporting highly potential wells in
production with gas stimulation and withdrawal from spending
for wells with no potentials. Each one of those scenarios could be studied with respect to the potential of production
under gas lift conditions. Here, we plan to study the effect of
the number of wells subject of study in an optimization issue
without restriction of entry gas. For this purpose, a full fivefactorial
trial design matrix was used. The optimization issues
with 0 to 5 wells involved in optimization issue were solved
by GA in accordance with the developed matrix. In addition
the total amount of gas consumption was calculated and the
results were listed in following table
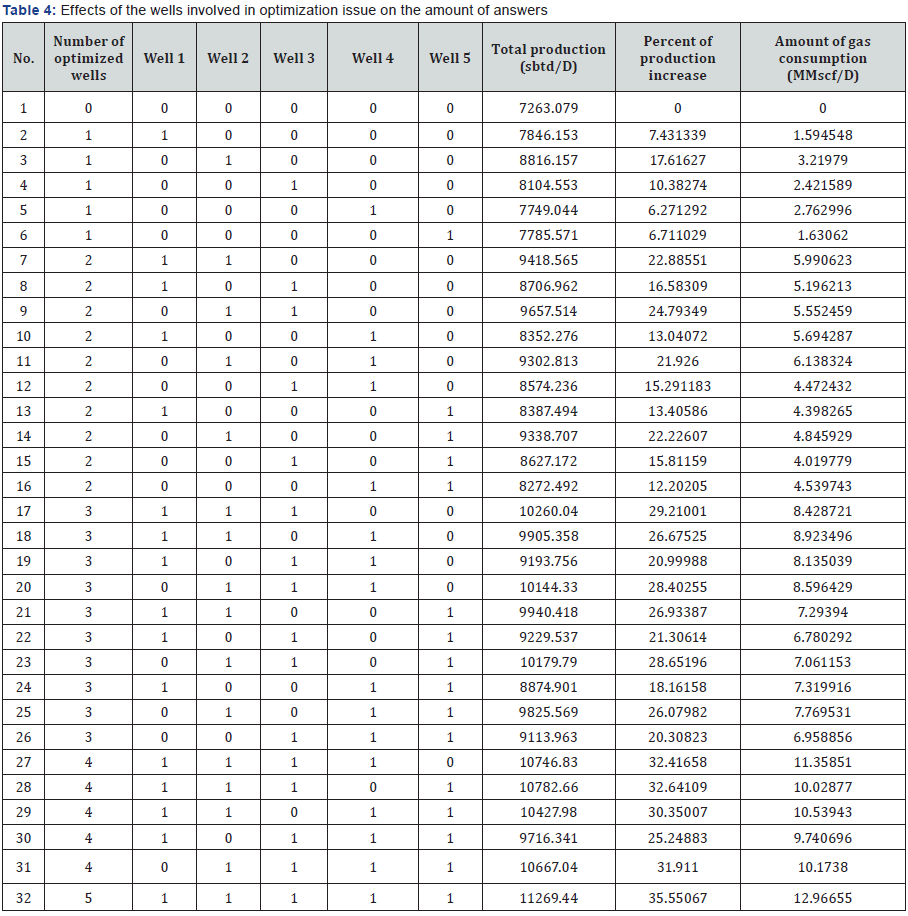
The results of (Table 4) show that by increase in number
of involved wells, the slope of production increase percentage
curve gradually moves down. In another word, for the present
five wells, it is predicted that infinite increase in the number
of wells subject of optimization will not cause an increase in
optimization output. In another word, in our study, increase in
the output caused by optimization has a limit and after reaching
that limit, the production increase percent will remain fixed.
Therefore, observations and calculations made by authors
emphasis that the irregular enlargement of the optimization
issue of gas lift does not contain economic profit especially
for the reason that the facilities and equipment of gas lift are
expensive and require using personnel of the utilization party.
In addition, enlarging optimization issue prolongs it and makes
it difficult to solve. Results of (Table 5) could be used to draw
Pareto diagram and determine the general effect of each well
on total amount of collection form series of wells. (Figure 3)
shows this diagram.
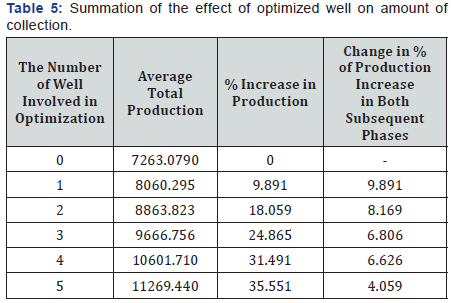

As it could be seen, the effects calculated for wells
correspondence with their potentials and since measuring
potentials of wells is easier, by considering the results of Table
4, it is suggested to take the optimization spaces as small as possible and in selecting the wells for optimization, consider
the potential factor.
Conclusion
The most important results obtained in recent research
are:
- Artificial neural networks have very good performance for modeling the process of gas lift and making performance curve of gas lift in comparison with classic methods.
- Linking the artificial neural networks (as proximate function) and genetic algorithm could be easily used in optimizing gas lift to oil wells.
- Optimization of the amount of oil production simultaneously, vs., gas consumption in a gas lift without restriction and with restriction is possible. Using new target functions, particularly sum of net products of wells and net total product has more economic value compared to classic views.
- Increase in number of wells involved in optimization issue does not necessarily cause linear increase in economic productivity of total wells. It seems there is a limit and desirable number for wells involved in optimization issue and this issue, along with the cost of equipment and man force generates needs to select the bet wells for as lift.
- The potential parameter could be used as a proposed parameter in selecting wells to be optimized in order to fill the index vacuum of selecting the well.
Acknowledgement
We take this opportunity to extend our best appreciation
to South Oil fields utilization Company for providing us with
the information of wells performance curves.
To
read more articles in Recent Advances in
Petrochemical Science
Please
Click on: https://juniperpublishers.com/rapsci/index.php



Comments
Post a Comment